Struktur Data
Struktur Data Graph
Graph
Graph adalah kumpulan dari simpul dan busur yang secara matematis dinyatakan sebagai :
G = (V, E)
Dimana
G = Graph
V = Simpul atau Vertex, atau Node, atau Titik
E = Busur atau Edge, atau arc
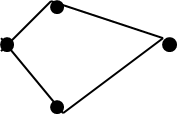
Contoh Graph:
V terdiri dari v1, v2, ... , v5
E terdiri dari e1, e2, ... , e7
Sebuah Graph belum tentu semua simpulnya terhubung dengan busur
Sebuah Graph mungkin mempunyai simpul yang tak terhubung dengan simpul yang lain
Sebuah Graph mungkin semua simpulnya saling berhubungan
Graph Berarah dan Graph Tak Berarah:
Dapat dilihat dari bentuk busur yang artinya urutan penyembutan pasangan 2 simpul
Graph tak Berarah (Undirected graph atau non-directed graph):
Urutan simpul dalam sebuah busur tidak dipentingkan. Mis busur e1 dapat disebut busur AB atau BA
Graph berarah (directed graph)
Urutan simpul mempunyai arti. Mis busur AB adalah e1 sedangkan busur BA adalah e8
Graph berbobot (weighted graph)
Jika setiap busur mempunyai nilai yang menyatakan hubungan antara 2 buah simpul, maka busur tersebut dinyatakan memiliki bobot.
Bobot sebuah busur dapat menyatakan panjang sebuah jalan dari 2 buah titik, jumlah rata rata kendaraan perhari yang melalui sebuah jalan, dll.
Graph Berbobot:
Jika e merupakan busur dengan simpul - simpulnya adalah v dan w ditulis e=(v,w), maka v dan w disebut "terletak" pada e, dan e disebut incident dengan v dan w
Degree (derajat), indegree dan outdegree
Degree sebuah simpul adalah jumlah busur yang incident dengan simpul tersebut.
Indegree sebuah simpul pada graph berarah adalah jumlah busur yang kepalanya incident dengan simpul tersebut, atau jumlah busur yang "masuk" atau menuju simpul tersebut
Outdegree sebuah simpul pada graph berarah adalah jumlah busur yang ekornya incident dengan simpul tersebut, atau jumlah busur yang "keluar" atau berasal dari simpul tersebut
Adjacent
Pada graph tidak berarah, 2 buah simpul disebut adjacent bila ada busur yang menghubungkan kedua simpul tersebut. Simpul V dan W disebut adjacent
Pada graph berarah, simpul V disebut adjacent dengan simpul W bila ada busur dari W ke V
Succesor dan Predecessor
Pada graph berarah, bila simpul V adjacent dengan simpul W, maka simpul V adalah succesor simpul W, dan simpul W adalah predecessor dari simpul V
Path
Sebuah path adalah serangkaian simpul - simpul yang berbeda, yang adjacent secara berturut - turut dari simpul satu ke simpul berikutnya
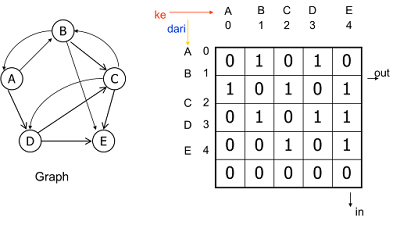
Representasi Graph dalam bentuk matrix
Adjacency Matrix Graph tak berarah
digambarkan sebagai simpul yang memiliki 2 pointer
Simpul vertex: Simpul edge:
Contoh: untuk vertex A, memiliki 2 edge yang terhubung yaitu e1 dan e2.
Adjency List Graph berarah
Graph berarah dan berbobot
Penyelesaian kasus Graph halaman sebelumnya:
- Define simpul untuk vertex dan edge
- Mengidentifikasi Simpul pertama sebagai vertex yang pertama
- Tambahkan vertex sisanya
- Tambahkan edge pada masing masing vertex yang telah terbentuk
- Tampilkan representasi graph berikut bobotnya
Sebuah Graph memiliki ciri berbeda dengan tree
Dalam Graph, edge bebas menghubungkan node-node mana pun.
Dalam Tree, satu node hanya boleh terhubung ke satu parent dan beberapa child, tidak boleh ke beberapa parent
Dalam sebuah Graph bisa dirunut jalur edge yang membentuk jalur putaran dari 1 node kembali ke node semula; ini tidak boleh terjadi dalam Tree
Spanning Tree
Spanning Tree adalah sebuah Tree yang dibuat dari sebuah Graph dengan menghilangkan beberapa edge-nya. Tree ini harus mengandung semua node yang dimiliki Graph
Jika Weighted Graph diubah menjadi Spanning Tree, tiap kombinasi Tree yang dapat dibuat memiliki total weight yang berbeda - beda
Problem Minimum Spanning Tree (MST) berusaha mencari Tree seperti apa yang bisa dibuat dari sebuah Weighted Graph dengan total weight seminimal mungkin.
MST Dengan Metode Greedy
Algortima Prim-Dijkstra
Ditemukan oleh Robert C. Prim di tahun 1957 dan oleh Edsger Dijkstra di tahun 1959
Algoritma Kruskal
Ditemukan oleh Joseph Kruskal ditahun 1956
Algoritma Kruskal
Langkah - langkah algoritma Kruskal:
- Asumsikan semua edge berwarna hitam
- Bandingkan bobot semua edge hitam, pilih edge dengan bobot terkecil
- Tandai edge yang dipilih dengan warna hjjau
- Apabila ada edge yang kedua node-nya sudah terkena jalur hijau, tandai edge tersebut dengan warna merah (karena jika dipilih akan membentuk jalur putaran a melanggar syarat tree)
- Ulangi dari langkah ke-2 hingga semua node terlewati jalur hijau
- Ketika semua node telah dilewati jalur hijau, maka jalur hijau yang terbentuk adalah MST yang dicari
Contoh Problem MST:
Dalam sebuah Graph yang setiap edge yang memiliki weight (bobot), jarak terpendek (shortest path) antara 2 node dapat dicari dengan metode Greedy
Misal kita hendak mencari jalur terpendek (Shortest Path) dari node A ke node F, bagaimana cara menghitungnya dengan Metode Greedy
Metode Greedy Shortest Path
Langkah - langkah Metode Greedy:
- Berangkat dari node awal
- Pilih edge yang memiliki bobot terkecil dari node tersebut
- Maju ke node yang dituju
- Ulangi dari langkah ke-2 hingga mencapai node tujuan
Solusi Optimal?
Benarkah solusi yang didapatkan dari Metode Greedy untuk Shortest Path Problem adalah benar - benar solusi terbaik?
Coba bandingkan solusi berikut:
Diskusikan mengapa bisa begitu?
Latihan
1. Buatlah Minimum Spanning Tree menggunakan algoritma Prim-Dijkstra dan algoritma Kruskal
2. Carilah Shortest Path dari Node A ke Node F dengan Metode Greedy!
3. Diskusikan mengapa kadang Metode Greedy gagal menghasilkan solusi terbaik!
4.Buatlah Minimum Spanning Tree menggunakan algoritma Prim-Djikstra dan Algoritma Kruskal
5. Carilah Shortest Path dari Node A ke Node I dengan Metode Greedy!































Komentar
Posting Komentar