Sorting

 Sorting

Pengertian

Pengurutan data dalam struktur data sangat penting untuk data yang bertipe data numerik ataupun karakter sehingga digunakan secara luas dalam aplikasi.

Pengurutan dapat dilakukan secara Ascending (naik) atau Decending (urut turun)

Pengurutan (Sorting) adalah proses menyusun kembali data yang sebelumnya telah disusun dengan pola tertentu, sehingga tersusun secara teratur menurut aturan tertentu.

Mengatur elemen berdasar urutan tertentu

Beberapa algoritma sorting telah dibuat karena proses tersebut sangat mendasar dan sering digunakan

Pengurutan data (Sorting) didefinisikan sebagai suatu proses untuk menyusun kembali himpunan obyek menggunakan aturan tertentu

Menurut Microsoft Book-self, definisi algoritma pengurutan adalah algoritma untuk meletakkan kumpulan elemen data ke dalam urutan tertentu berdasaran satu atau beberapa kunci dalam tiap - tiap elemen

Dua macam Aturan

Ada dua macam urutan yang biasa digunakan dalam proses pengurutan yaitu:

    1. Urut naik (Ascending) yaitu dari data yang mempunyai nilai paling kecil sampai paling besar

    2. Urut turun (Descending) yaitu data yang mempunyai nilai paling besar sampai kecil

Contoh

Data bilangan 5, 2, 6 dan 4

    Dapat diurutkan naik menjadi 2, 4, 5, 6

    atau

    Dapat diurutkan turun menjadi 6, 5, 4, 2

Manfaat

Keuntungan dari data yang terurut antara lain:

    Data muda dicari (misalnya dalam buku telepon atau kamus bahasa), mudah untuk dibetulkan,                 dihapus, disisipi atau digabungkan

    Mudah melakukan pengecekan apakah ada data yang hilang

    Melakukan kompilasi program komputer jika tabel - tabel simbol harus dibentuk

    Mempercepat proses pencarian data yang harus dilakukan berulang kali

Faktor yang mempengaruhi pada efektifitas Sorting

• Banyak data yang diurutkan
• Kapasitas pengingat apakah mampu menyimpan semua data yang kita miliki
• Tempat penyimpanan data, misalnya piringan, pita atau kartu, atau media penyimpanan yang lain.

Bubble Sort

Metode Sorting termudah, Diberi nama "Bubble" karena proses pengurutannya secara berangsur - angsur bergerak/berpindah ke posisinya yang tepat, seperti gelembung yang keluar dari sebuah gelas bersoda.

Bubble sort mengurutkan data dengan cara membandingkan elemen sekarang dengan elemen berikutnya.

Pengurutan Ascending: Jika elemen sekarang lebih besar dari elemen berikutnya maka kedua elemen tersebut ditukar

Pengurutan Descending: Jika elemen sekarang lebih kecil dari elemen berikutnya, maka kedua elemen tersebut ditukar

Algoritma ini seolah-olah menggeser satu per satu elemen dari kanan ke kiri atau kiri ke kanan, tergantung jenis pengurutannya, asc atau desc

Ketika satu proses telah selesai, maka bubble sort akan mengulangi proses, demikian seterusnya sampai dengan iterasi sebanyak n-1.

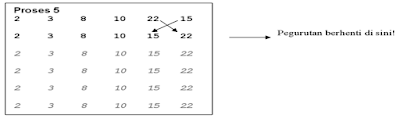
Kapan berhentinya? Bubble sort berhenti jika seluruh array telah diperiksa dan tidak ada pertukaran lagi yang bisa dilakukan, serta tercapai perurutan yang telah diinginkan

INSERTION SORT

Mirip dengan cara orang mengurutkan kartu, selembar demi selembar kartu diambil dan disisipkan (insert) ke tempat yang seharusnya

Pengurutan dimulai dari data ke-2 sampai dengan data terakhir, jika ditemukan data yang lebih kecil, maka akan ditempatkan (diinsert) diposisi yang seharusnya.

Pada penyisipan elemen, maka elemen- elemen lain akan bergeser ke belakang

Insertion sort: Algoritma

Bagi elemen data yang akan diurutkan menjadi dua

    - Bagian yang belum diurutkan

    - Bagian yang telah diurutkan

Ulangi langkah tersebut hingga tidak ada elemen tersisa dalam array

    - Elemen pertama dipilih dari bagian yang belum diurutkan

    - Tempat elemen terpilih sesuai urutan pada array

Selection Sort

Merupakan kombinasi antara sorting dan searching

Untuk setiap proses, akan dicari elemen - elemen yang belum diurutkan yang memiliki nilai terkecil atau terbesar akan dipertukarkan ke posisi yang tepat di dalam array

Misalnya untuk putaran pertama, akan dicari data dengan nilai terkecil dan data ini akan ditempatkan di indeks terkecil (data[0]), pada putaran kedua akan dicari data kedua terkecil, dan akan ditempatkan di indeks kedua (data[1]).

Selama proses, pembandingan dan pengubahan hanya dilakukan pada indeks pembandingan saja, pertukaran data secara fisik terjadi pada akhir proses

Selection Sort: Algoritma

Pilih elemen dengan nilai terendah

Tukarkan elemen terpilih dengan elemen pada posisi ke - i

    - i dimulai dari 1 hingga n

    - Dimana n adalah total elemen yang ada dikurangi 1

Merge Sort

Merge sort merupakan algoritma pengurutan dalam ilmu komputer yang dirancang untuk mmenuhi kebutuhan pengurutan atas suatu rangkaian data yang tidak memungkinkan untuk ditampung dalam memori kokmputer karena jumlahnya yag terlalu besar.

Algoritma ini ditemukan oleh John von Neumann pada tahun 1945

Algoritma Merge Sort

Prinsip utama yang diimplementasikan pada alogirtma merge-sort seringkali disebut sebagai pecah belah dan taklukkan (bahasa inggris: divide and conquer).

Cara kerja algoritma merge sort adalah membagi larik data yang diberikan menjadi dua bagian yang lebih kecil. Kedua larik yang baru tersebut kemudian akan diurutkan secara terpisah.

Setelah kedua buah list tersusun, maka akan dibentuk larik baru sebagai hasil penggabungan dari dua buah larik sebelumnya.

Contoh Penerapan

Data sumber yang akan diurutkan adalah sebagai berikut: {3, 9, 4, 1, 5, 2}:

Larik tersebut dibagi menjadi dua bagian, {3, 9, 4} dan {1, 5, 2}

Kedua larik kemudian dirutkan secara terpisah sehingga menjadi {3, 4, 9} dan {1, 2, 5}

Sebuah larik kemudian dibentuk yang sebagai penggabungan dari kedua larik tersebut {1}, semenntara nilai - nilai dalam masing larik {3, 4, 9} dan {2, 5} (nilai 1 dalam elemen larik ke dua telah dipindahkan ke larik baru)

Langkah berikutnya adalah penggabungan dari masing masing larik ke dalam larik baru yang dibuat sebelumnya.

Quick Sort

Metode quick sort adalah metode pengurutan yang menggunakan partisi.

Pada metode ini, data dibagi menjadi dua bagia, yaitu data disebelah kiri partisi selalu lebih kecil dari data disebelah kanan. Proses pengurutan dilakukan pada kedua partisi secara terpisah

Algoritma Quicksort

Tentukan unsur partisi yang diperlukan (gunakan data tengah sebagai unsur partisi)

Partisi data dalam dua bagian yang dipisahkan oleh unsur partisi

Secara rekursif sort terhadap kedua bagian data diatas dengan metode partisi (ulangi langkah 1 dan 2 untuk data sebelah kiri dan kanan).

Contoh

Diberikan data berikut : 44 - 55 - 12 - 42 - 94 - 6 - 18 - 67

Unsur partisi yang digunakan adalah 42 yang merupakan data tengah pada deretan data tersebut. Dengan menggunakan prosedur partisi urutan data menjadi:

18 - 6 - 12 - 42 - 94 - 55 - 44 - 67

Data 18, 6, 12 lebih kecil dari 42 dan data 94, 55, 44, 67 lebih besar dari 42

Data kiri: 18 6 12

Data kanan: 42 94 55 44 67

Untuk data kiri dilakukan partisi lagi, unsur partisinya adalah 6

Sub data kiri: tidak ada karena tidak ada data yang lebih kecil dari 6

Sub data kanan: 6 12 18

Untuk sub data kanan dilakukan partisi lagi, unsur partisinya adalah 12.

Ssub data kiri: 6

Sub data kanan : 12 18

Proses rekursif selesai dan data telah terurut.

Proses partisi untuk data kanan.

Data disebelah kanan di partisi lagi, dengan unsur partisinya adalah 55

Sub data kiri: 44 42

Sub data kanan: 55 94 67

Untuk sub data kiri dilakukan partisi lagi, dengan unsur partisinya adalah 44

Sub data kiri: 42

Sub data kanan: 44

Untuk sub data kanan dilakukan partisi lagi, dengan unsur partisinya adalah 94

Sub data kiri: 67 55

Sub data kanan: 94

Selanjutnya, dilakukan partisi lagi, dengan unsur partisinya adaah 67

Sub data kiri: 55

Sub data kanan: 67

Proses rekursif untuk tabel kanan selesai

data setelah pengurutan menjadi: 6 12 18 42 55 67 94

Latihan

1.    12, 22, 8, 19, 19, 10, 9, 20 (menggunakan bubble sort dan insertion sort)

2.    2, 3, 4, 5, 50, 10, 15, 13 (menggunakan selection sort dan quick sort)